What is Maelstrom?¶
Maelstrom is a code that enables the modelling and analysis of binary light curves with a pulsating component. When a pulsating star is in orbit with a companion, the time taken for the stellar pulsations to reach us changes over time. This information is encoded in the phase of the pulsation, which, for the coherently pulsating \(\delta\) Scuti stars can be used as clocks to infer the position of the stars throughout the orbit.
This method is known as phase modulation. Phase modulation has been used for a wide range of stars, most notable of which being pulsars, whose highly precise millisecond level precision enabled the detection of the first planet. For intermediate mass stars, phase modulation is useful for the A/F type pulsators to infer stellar mass companions.
The Maelstrom code contains routines for forward modelling these orbits. In a forward model, a light curve is generated from the orbital parameters and fit to the actual light curve data.
Getting started¶
[1]:
import numpy as np
import corner
import pandas as pd
import matplotlib.pyplot as plt
import exoplanet as xo
import pymc3 as pm
import lightkurve as lk
[2]:
%config IPython.matplotlib.backend = "retina"
from matplotlib import rcParams
rcParams["figure.dpi"] = 150
rcParams["savefig.dpi"] = 150
In this notebook, we’re going to inspect and fit the time delays for a well known Kepler \(\delta\) Scuti system, KIC 9651065. This tutorial assumes basic working knowledge of PyMC3. A great introduction to this can be found here
Now, let’s first download the light curve.
[3]:
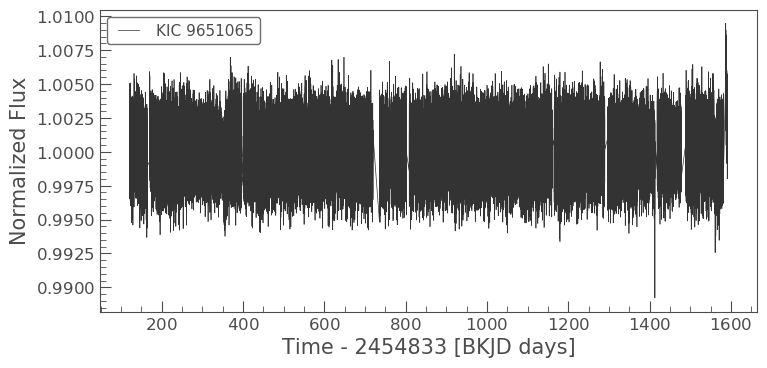
lc = lk.search_lightcurvefile('KIC 9651065', mission='Kepler').download_all().PDCSAP_FLUX.stitch().remove_nans()
lc.plot()
[3]:
<matplotlib.axes._subplots.AxesSubplot at 0x114a3f828>
Note
Lightkurve automatically subtracts the Kepler zero time (2454844 days), so all times are reported in Barycentric Kepler Julian Date (BKJD). If you want to include additional data, you must work within the same reference time.
Here, we pass the time and flux data into Maelstrom. If the freq argument is not specified, Maelstrom will automatically try and detect some good peaks to use. Be warned however, this does not always work and you should always check which frequencies you use! I have set the upper limit on the peak search to 40 d\(^{-1}\), since there are some Nyquist aliases. We can tell they are aliases as their time delays will match the Kepler orbital period. Neat!
first_look will subdivide the lightcurve using the old method, and make some diagnostic plots. In order, these are the light curve, the amplitude spectrum, the extracted time delays, and the periodogram of the time delays. The frequencies are colored by their amplitude, and the orange line is the weighted average value. We see a nice peak around 272 d in the last panel, which is the orbital period of the system.
[6]:
from maelstrom import Maelstrom
ms = Maelstrom(lc.time, lc.flux, max_peaks=3, fmin=5, fmax=40)
ms.first_look();
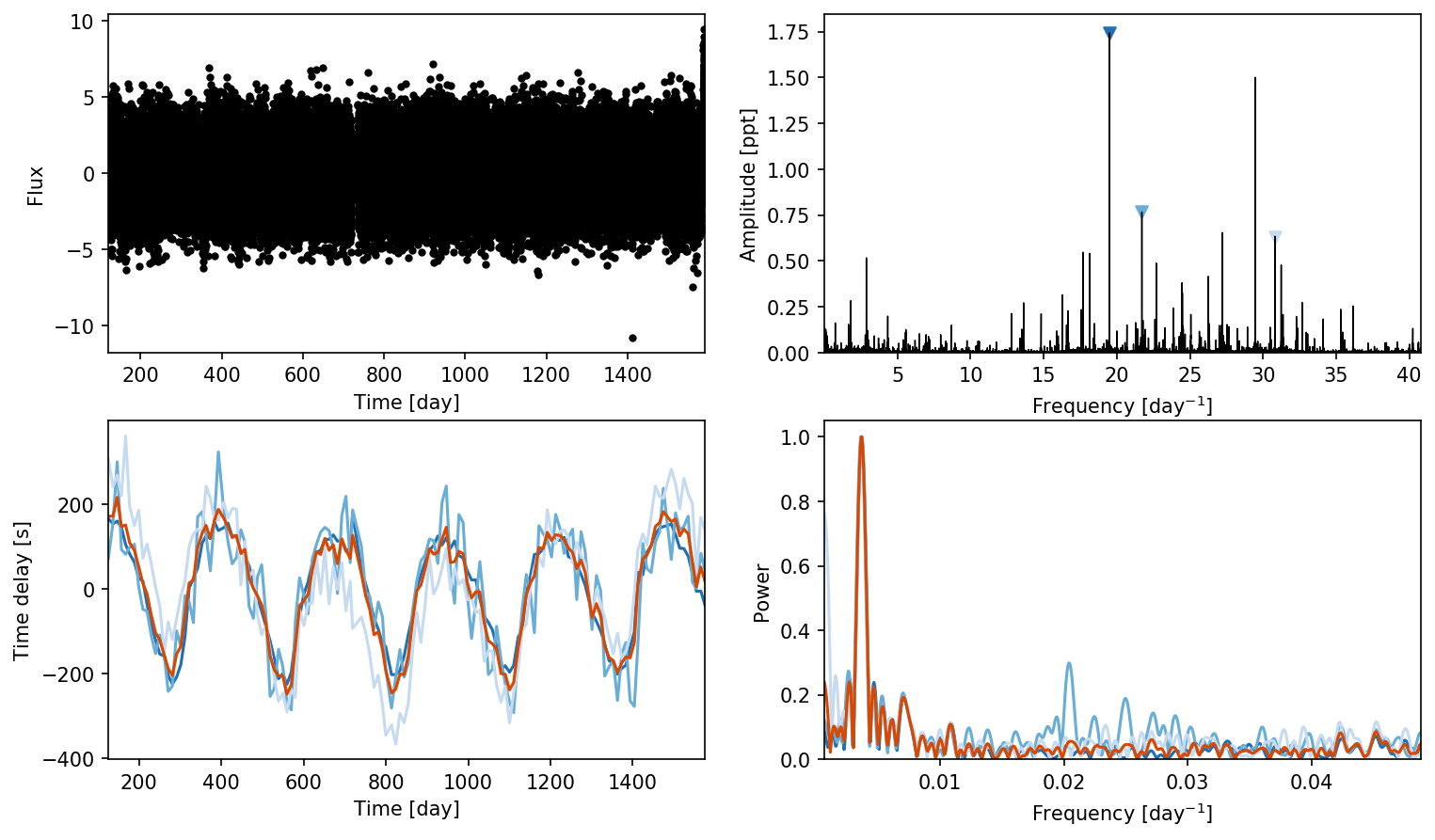
Note that if you want the frequencies Maelstrom has found, simply call ms.freq
[14]:
print(f"Oscillation modes are at {ms.freq}")
Oscillation modes are at [19.47767606 21.71213419 30.80189468]
To read off this period, we can calculate the peak in the power spectrum of the time delays (the bottom left panel above)
[9]:
period_guess = ms.get_period_estimate()
print(f"The orbital period is around {period_guess:.2f} days")
The orbital period is around 269.96 days
This is pretty good for a few lines of code! In fact, the actual orbital period is closer to 272 d.
Let’s now perform an initial optimisation.. We first need to call setup_orbit_model, but an orbital period estimate is not required (unless the time delay signal is very weak..!). We can also pass along an initial guess for the eccentricity, but let’s leave it at 0 and see what happens.
[12]:
ms.setup_orbit_model(period=period_guess)
opt = ms.optimize()
[13]:
opt
[13]:
{'logperiod': array(5.60521922),
't0': array(15.39716591),
'varpi_angle__': array([ 3.64010862, -2.59799919]),
'eccen_interval__': array(-0.19682975),
'logs': array(0.21291598),
'lighttime': array([178.34565426, 191.30015751, 193.97131511]),
'mean_flux': array(0.00075224),
'W_hat_cos': array([ 1.7414353 , 0.46678714, -0.59316665]),
'W_hat_sin': array([ 0.2940882 , 0.62832883, -0.28794189]),
'period': array(271.84151162),
'varpi': array(2.19066763),
'eccen': array(0.4509518),
'tref': array(24.82834397)}
Let’s go through some of those parameters for a sec. The ones not mentioned are nuisance parameters which are required for the model.
t0: Time of periastron passage (d)lighttime: The projected semi-major axis calculated for each frequency in the model. Note that most of these agree, indicating that all the frequencies in theMaelstrommodel belong to the same star.period: The orbital period of the system.varpi: The angle between the ascending node and periapsiseccen: Orbital eccentricitytref: Time of reference passage of periapsis
Let’s see what the theoretical time delays look like in the optimised model vs the actual extracted values.
[20]:
td_time, td_td = ms.get_time_delay()
td_average = np.average(td_td, axis=-1, weights=ms.get_weights())
[21]:
with ms:
model_td = xo.eval_in_model(ms.tau, opt) * 86400
plt.plot(ms.time, model_td - np.median(model_td), c='blue', linewidth=0.5)
plt.plot(td_time, td_average, '.k')
plt.xlabel('Time [day]')
plt.ylabel('Time delay [s]')
[21]:
Text(0, 0.5, 'Time delay [s]')
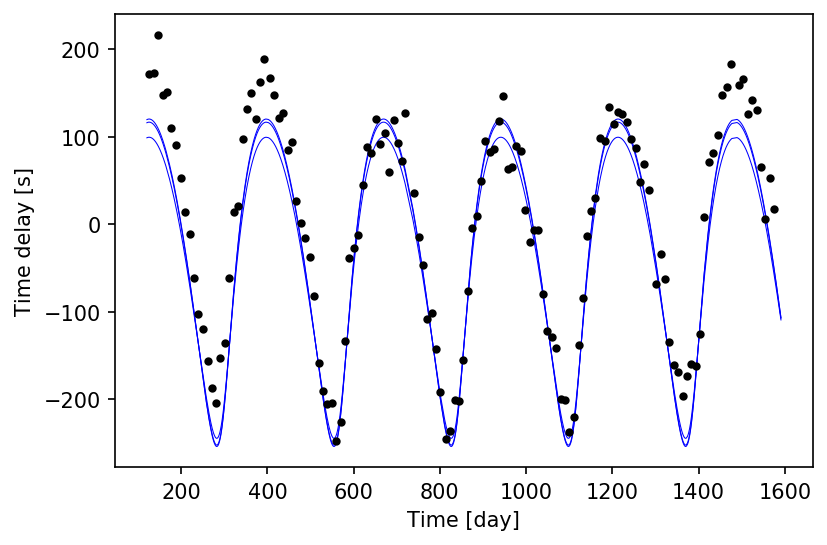
Cool! Each frequency in the light curve has its own independent asini in the Maelstrom model. This is useful for when there are multiple stars pulsating in the same binary system, as they would be (mostly) equal and opposite in sign.
However, Maelstrom isn’t actually fitting these parameters. What we’re doing is forward modelling the input light curve by fitting the phase variations (\(\tau\)) in each point;
\(y(t) = \sum_{j=1}^{J} \Big[A_j \cos(\omega_j (t - \tau)) + B_j \sin(\omega_j (t-\tau))\Big]\)
Although it is not as useful as looking at the time-delays, we can still inspect the actual light curve that is generated from the time delay signal:
[22]:
with ms:
plt.plot(ms.time, xo.eval_in_model(ms.lc_model, opt), c='blue', linewidth=0.5, label='Maelstrom')
plt.plot(ms.time, ms.flux, '.k', label='Data')
plt.xlim(200,205)
plt.xlabel('Time [day]')
plt.ylabel('Flux [ppt]')
plt.legend()
[22]:
<matplotlib.legend.Legend at 0x132291860>

Maelstrom has decided that all these frequencies belong to one star, as their lighttimes are all positive (or negative). This means the system is PB1. We can get a ready-made model from the get go by asking nicely, and passing in the optimisation results. The PB1 model is for binaries with only one pulsating component. All the frequencies now use the same asini parameter, unlike our first model
[24]:
pb1_model = ms.pin_orbit_model(opt)
pb1_model
[24]:
As we can see, pb1_model inherits from the PyMC3 Models object. It is, by definition, a custom model which has access to all of the properties of the default Model class. This means we can do cool things like this:
[25]:
pm.model_to_graphviz(pb1_model)
[25]:
Finally, if we are happy with the default priors in Maelstrom we can sample the model. There are strong covariances between some of the parameters. This means that sampling will slow down significantly unless we use a custom NUTS step (see https://exoplanet.dfm.io/en/stable/tutorials/pymc3-extras/#dense-mass-matrices)
Sampling is quite slow while the mass matrix is tuned (typically the first 1000 steps). Because of this, I’m only going to make 10 draws of the posterior distribution.
[27]:
trace = pb1_model.sample(tune=10, draws=10)
optimizing logp for variables: [PB1_mean]
4it [00:00, 22.28it/s, logp=-1.150728e+05]
message: Optimization terminated successfully.
logp: -115072.80884284787 -> -115072.7881902971
optimizing logp for variables: [PB1_logs_lc]
8it [00:00, 27.62it/s, logp=-1.097041e+05]
message: Optimization terminated successfully.
logp: -115072.7881902971 -> -109704.06934437387
optimizing logp for variables: [PB1_omega, PB1_eccen]
45it [00:01, 26.08it/s, logp=-1.066786e+05]
message: Optimization terminated successfully.
logp: -109704.06934437387 -> -106678.6001791905
optimizing logp for variables: [PB1_phi]
20it [00:00, 26.86it/s, logp=-1.066570e+05]
message: Optimization terminated successfully.
logp: -106678.6001791905 -> -106657.04265097293
optimizing logp for variables: [PB1_lognu]
103it [00:03, 32.85it/s, logp=-1.066545e+05]
message: Desired error not necessarily achieved due to precision loss.
logp: -106657.04265097293 -> -106654.54220594438
optimizing logp for variables: [PB1_eccen, PB1_omega, PB1_lognu, PB1_mean, PB1_logasini, PB1_logs_lc, PB1_phi, PB1_logP]
323it [00:11, 27.99it/s, logp=-1.064707e+05]
message: Desired error not necessarily achieved due to precision loss.
logp: -106654.54220594438 -> -106470.71703961623
optimizing logp for variables: [PB1_logasini]
67it [00:02, 32.72it/s, logp=-1.064707e+05]
message: Desired error not necessarily achieved due to precision loss.
logp: -106470.71703961623 -> -106470.71703961623
optimizing logp for variables: [PB1_eccen, PB1_omega, PB1_lognu, PB1_mean, PB1_logasini, PB1_logs_lc, PB1_phi, PB1_logP]
81it [00:02, 27.78it/s, logp=-1.508331e+05]
message: Desired error not necessarily achieved due to precision loss.
logp: -106470.71703961623 -> -106470.71703961623
optimizing logp for variables: [PB1_logP]
4it [00:00, 23.40it/s, logp=-1.064707e+05]
message: Optimization terminated successfully.
logp: -106470.71703961623 -> -106470.71703961515
optimizing logp for variables: [PB1_eccen, PB1_omega, PB1_lognu, PB1_mean, PB1_logasini, PB1_logs_lc, PB1_phi, PB1_logP]
133it [00:04, 28.31it/s, logp=-1.064707e+05]
message: Desired error not necessarily achieved due to precision loss.
logp: -106470.71703961515 -> -106470.71703961305
Only 10 samples in chain.
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [PB1_eccen, PB1_omega, PB1_lognu, PB1_mean, PB1_logasini, PB1_logs_lc, PB1_phi, PB1_logP]
Sampling 2 chains: 100%|██████████| 40/40 [00:59<00:00, 1.49s/draws]
/Users/danielhey/anaconda3/lib/python3.7/site-packages/pymc3/sampling.py:464: UserWarning: The number of samples is too small to check convergence reliably.
warnings.warn("The number of samples is too small to check convergence reliably.")
There were 7 divergences after tuning. Increase `target_accept` or reparameterize.
The acceptance probability does not match the target. It is 0.06641073900830238, but should be close to 0.9. Try to increase the number of tuning steps.
There were 7 divergences after tuning. Increase `target_accept` or reparameterize.
The acceptance probability does not match the target. It is 2.2473988127317096e-06, but should be close to 0.9. Try to increase the number of tuning steps.
Look at all those errors! That’s because we only sampled for 10 steps across 2 chains. For a full sampling run, check out the case studies in the sidebar.
In any case, our trace is a PyMC3 trace object which can be manipulated accordingly:
[28]:
pm.summary(trace)
/Users/danielhey/anaconda3/lib/python3.7/site-packages/pymc3/stats.py:991: FutureWarning: The join_axes-keyword is deprecated. Use .reindex or .reindex_like on the result to achieve the same functionality.
axis=1, join_axes=[dforg.index])
[28]:
| mean | sd | mc_error | hpd_2.5 | hpd_97.5 | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|
| PB1_logs_lc | 0.212922 | 8.600234e-06 | 2.719611e-06 | 0.212913 | 0.212931 | NaN | 234.349313 |
| PB1_mean | 0.000748 | 9.571820e-06 | 3.026826e-06 | 0.000739 | 0.000758 | NaN | 103.871715 |
| PB1_lognu__0 | 2.969269 | 3.418779e-08 | 1.057404e-08 | 2.969269 | 2.969269 | NaN | 4.133664 |
| PB1_lognu__1 | 3.077871 | 1.183244e-07 | 3.247042e-08 | 3.077871 | 3.077872 | NaN | 1.318653 |
| PB1_lognu__2 | 3.427576 | 6.475697e-08 | 1.901471e-08 | 3.427576 | 3.427576 | NaN | 1.087233 |
| PB1_logP | 5.605784 | 7.644901e-06 | 2.417445e-06 | 5.605777 | 5.605792 | NaN | 69.104374 |
| PB1_period | 271.995197 | 2.079376e-03 | 6.575335e-04 | 271.993118 | 271.997319 | 1.052922 | 69.103851 |
| PB1_phi | 0.569194 | 2.178819e-06 | 6.889910e-07 | 0.569192 | 0.569196 | NaN | 120.295888 |
| PB1_logasini | 5.221367 | 1.418273e-05 | 4.484865e-06 | 5.221352 | 5.221381 | NaN | 72.400180 |
| PB1_asini | 185.187119 | 2.626459e-03 | 8.305392e-04 | 185.184426 | 185.189745 | 1.052904 | 72.401205 |
| PB1_nu__0 | 19.477680 | 6.658988e-07 | 2.059578e-07 | 19.477679 | 19.477681 | NaN | 4.133665 |
| PB1_nu__1 | 21.712135 | 2.569075e-06 | 7.050022e-07 | 21.712132 | 21.712139 | 3.268674 | 1.318653 |
| PB1_nu__2 | 30.801896 | 1.994638e-06 | 5.856890e-07 | 30.801893 | 30.801898 | 4.569588 | 1.087233 |
| PB1_omega | 2.201137 | 5.935100e-07 | 1.876577e-07 | 2.201136 | 2.201138 | NaN | 30.042722 |
| PB1_eccen | 0.457221 | 7.910098e-07 | 2.500954e-07 | 0.457220 | 0.457222 | 1.054756 | 25.987299 |
[ ]: